Teorema de "rolle"

En cálculo diferencial,  el teorema de Rolle demuestra la existencia de un punto interior en un intervalo abierto para el cual la derivada de una función derivable se anula cuando el valor de ésta en los extremos del intervalo es el mismo. Es generalizado mediante el teorema del valor medio, del que este es un caso especial. Es uno de los principales teoremas en cálculo debido a sus aplicaciones.


En el siguiente gráfico se observan las tres condiciones: la función es continua en el intervalo cerrado [a,b], es derivable y los valores que toma la función en los puntos a y b son iguales, es decir, f(a) = f(b). Existe, por lo tanto, al menos un punto c que pertenece al intervalo abierto (a,b) en el cual la derivada de la función es igual a cero. Vale observar que c es distinto de a y de b. No debemos confundir c con f(c), que sí puede ser igual a f(a) y f(b).

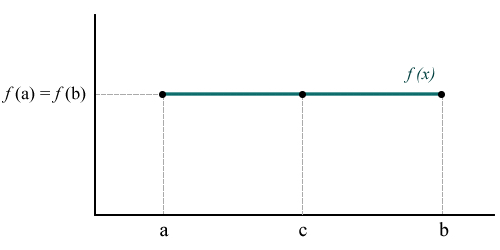
En la ilustración se ve una función constante, pero el teorema no sólo se cumple en este caso. Se pueden dar tres casos en los que f(c) es distinto de f(a) y f(b), a saber:
Caso 1. El punto máximo es igual a f(a) y f(b) y el punto mínimo es distinto de ambos, lo cual implica que la curva es cóncava hacia arriba. El punto mínimo es m = f(c), y la derivada de la función en este punto es 0.

Caso 2. El punto mínimo es igual a f(a) y f(b) y el punto máximo es distinto de ambos, lo cual implica que la curva es cóncava hacia abajo (o convexa). El punto máximo es M = f(c), y la derivada de la función en este punto es 0.

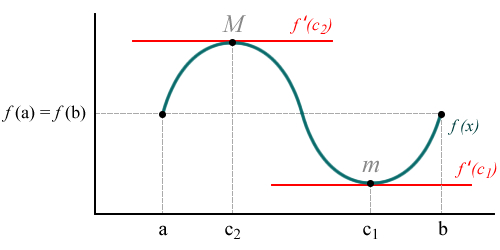
Caso 3. Tanto el punto mínimo como el punto máximo son distintos a f(a) y f(b). Esto significa que dentro del intervalo cerrado [a, b] la función alcanza un punto máximo M = f(c₂) mayor al valor de la función en los extremos a y b y un punto mínimo m = f(c₁) menor a los mismos. Tanto en el punto máximo como en el punto mínimo, la derivada de la función es nula. Es decir, f '(c₁) = 0 y f '(c₂) = 0.