MAXIMOS Y MINIMOS RELATIVOS
Entre los valores q puede tener una función (Y) puede haber uno que sea el mas grande y otro que sea el mas pequeño. A estos valores se les llama respectivamente punto máximo y punto mínimo absolutos.
Si una función continua es ascendente en un intervalo y a partir de un punto cualquiera empieza a decrecer, a ese punto se le conoce como punto critico máximo relativo, aunque comúnmente se le llama solo máximo.
Por el contrario, si una funcion continua es decreciente en cierto intervalo hasta un punto en el cual empieza a ascender, a este punto lo llamamos puntro critico minimo relativo, o simplemente minimo.
Una funcion puede tener uno, ninguno o varios puntos criticos.
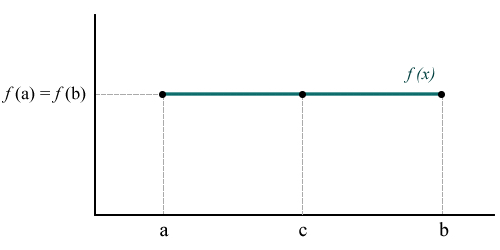
Curva sin máximos ni mínimos función sin máximos ni mínimos
Función con un máximo curva con un máximo y un mínimo
Curva con un mínimo curva con varios mínimos y máximos
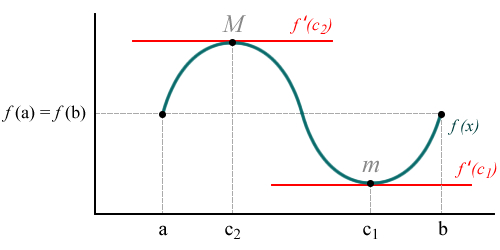
La pendiente de la recta tangente a una curva (derivada) en los puntos críticos máximos y mínimos relativos es cero, ya que se trata de una recta horizontal.
En los puntos críticos máximos, las funciones tienen un valor mayor que en su entorno, mientras que en los mínimos, el valor de la función es menor que en su entorno.
En un punto critico maximo relativo, al pasar la funcion de creciente a decreciente, su derivada pasa de positiva a negativa.
En un punto critico minimo relativo, la función deja de decrecer y empieza a ser creciente, por tanto, su derivada pasa de negativa a positiva.
METODOS PARA CALCULAR MAXIMOS Y MINIMOS DE UNA FUNCION
CRITERIO DE LA PRIMERA DERIVADA, UTILIZADO PARA UNA FUNCION CONTINUA Y SU PRIMERA DERIVADA TAMBIEN CONTINUA.
Este procedimiento consiste en:
Si el resultado fuera cero, no se puede afirmar si hay o no un máximo o mínimo.
APLICACIÓN DE MAXIMOS Y MINIMOS RELATIVOS EN LA SOLUCION DE PROBLEMAS
Para resolver los problemas a partir de los datos existentes, es importante en primer lugar, encontrar la expresión matemática de la función que represente el problema y cuyos valores máximos o mínimos se desean obtener.
Si la expresión matemática contiene varias variables, deberá plantearse en función de una sola; las condiciones del problema deben aportar suficientes relaciones entre las variables, para poderse expresar a todas ellas en función de una sola variable independiente.
Una vez que se tenga la función en la forma Y=f(X), se aplican las normas ya estudiadas.
En muchos problemas prácticos resulta muy sencillo identificar cuales valores críticos dan máximos o mínimos; y en consecuencia, ya no será necesario aplicar el procedimiento completo.
Es conveniente construir la grafica que represente la función en cuestión, a fin de verificar los resultados obtenidos.
PROBLEMAS