CONCEPTO DE DERIVADA
En matemática, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el limite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.La derivada de una función
 es la pendiente geométrica de la recta tangente del gráfico de
es la pendiente geométrica de la recta tangente del gráfico de  en
en  . Sin el concepto que se va a definir, no es posible encontrar directamente la pendiente de la línea tangente a una función dada, porque solamente se conoce un punto en la línea tangente:
. Sin el concepto que se va a definir, no es posible encontrar directamente la pendiente de la línea tangente a una función dada, porque solamente se conoce un punto en la línea tangente: 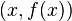 . La idea es aproximar la línea tangente con múltiples líneas secantes que tienen distancias progresivamente más pequeñas entre los dos puntos que cruzan. Cuando se toma el límite de las pendientes de las líneas secantes de esta progresión, se consigue la pendiente de la línea tangente.
. La idea es aproximar la línea tangente con múltiples líneas secantes que tienen distancias progresivamente más pequeñas entre los dos puntos que cruzan. Cuando se toma el límite de las pendientes de las líneas secantes de esta progresión, se consigue la pendiente de la línea tangente.PROPIEDADES DE LAS DERIVADAS
La mayor parte de los cálculos de derivadas requieren tomar eventualmente la derivada de algunas funciones comunes. La siguiente lista incompleta proporciona algunas de las más frecuentes funciones de una variable real usadas y sus derivadas.
- Derivada de potencias: si
donde r es cualquier número real, entonces
donde quiera que esta función sea definida. Por ejemplo, si 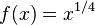 , entonces
, entonces
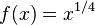 , entonces
, entonces
y la función derivada es definida sólo para números positivos x, no para x = 0. Cuando r = 0, esta regla implica que f′(x) es cero para x ≠ 0, lo que la convierte en la regla de la constante (expuesta abajo).
ejercicios de derivación
Funciones exponenciales y logarítmicas:
funciones trigonométricas:
Funciones trigonométricas inversas:
Reglas prácticas de derivación
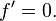
- Regla de la suma:
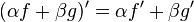 para toda función f y g y todo número real
para toda función f y g y todo número real  y
y  .
.- Regla del producto:
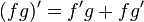 para toda función f y g. Por extensión, esto significa que la derivada de una constante multiplicada por una función es la constante multiplicada por la derivada de la función. Por ejemplo,
para toda función f y g. Por extensión, esto significa que la derivada de una constante multiplicada por una función es la constante multiplicada por la derivada de la función. Por ejemplo, 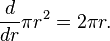
- Regla del cociente:
 para toda función f y g para todos aquellos valores tales que g ≠ 0.
para toda función f y g para todos aquellos valores tales que g ≠ 0.- Regla de la cadena: Si
 , siendo que derivable en "x", y "h" derivable en g(x), entonces.
, siendo que derivable en "x", y "h" derivable en g(x), entonces.
Ejemplo de cálculo
La derivada de
es
Aquí, el segundo término se calculó usando la regla de la cadena y el tercero usando la regla del producto. La derivadas conocidas de funciones elementales x2, x4, sin(x), ln(x) y exp(x) = ex, así como la constante 7, también fueron usadas
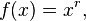

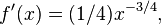



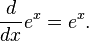

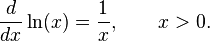
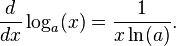
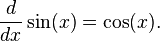

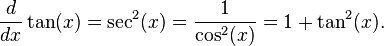
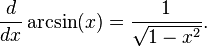
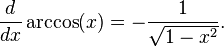

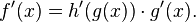

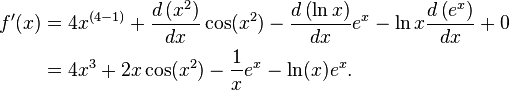
No hay comentarios:
Publicar un comentario